L’explosion des données, la sophistication croissante des systèmes à modéliser, et les limites physiques des processeurs traditionnels ont placé la complexité algorithmique au cœur des préoccupations contemporaines. Face à cette complexité, la distinction entre les approches classiques et quantiques n’est plus une simple affaire de performance. Elle révèle deux visions fondamentalement différentes du calcul.
Alors que le paradigme classique repose sur une exploration séquentielle ou heuristique des possibles, le paradigme quantique propose une exploration parallèle fondée sur les principes de superposition, d’intrication et d’interférence. Cette divergence ne relève pas seulement de la théorie : elle engage la manière dont on envisage le traitement de l’information, l’optimisation, la simulation scientifique, et plus largement l’avenir de la connaissance computationnelle.
Le mur algorithmique du calcul classique
Depuis les débuts de l’informatique moderne, la complexité algorithmique a constitué à la fois un moteur de progrès et une frontière infranchissable. La majorité des systèmes que nous cherchons à modéliser ou à résoudre – qu’il s’agisse d’un planning d’optimisation logistique, de l’analyse de grands graphes de réseaux sociaux, ou de problèmes de physique moléculaire – obéissent à des dynamiques combinatoires où les configurations croissent de manière explosive avec la taille du problème. Pour un problème à n variables binaires, le nombre d’états possibles est de 2ⁿ. Autrement dit, chaque variable supplémentaire double l’espace à explorer.
Cette croissance exponentielle est la signature des problèmes dits NP-difficiles. Les algorithmes classiques, même les plus avancés, voient alors leur temps d’exécution croître de façon exponentielle. Des méthodes heuristiques, des approximations ou du calcul parallèle permettent parfois de repousser temporairement l’échéance, mais ne suffisent plus à mesure que la dimension des données explose.
Prenons pour illustration un graphique simple mais révélateur : si l’on représente en échelle logarithmique le temps de calcul nécessaire pour résoudre un problème d’optimisation en fonction du nombre de variables, on observe deux courbes très différentes. Celle du calcul classique suit une croissance exponentielle, traduisant la difficulté inhérente à parcourir un espace de solutions trop vaste. Celle du calcul quantique, en revanche, dans certains cas – comme avec l’algorithme de Grover – ne croît que quadratiquement. L’écart devient gigantesque à partir de seulement quelques dizaines de variables.
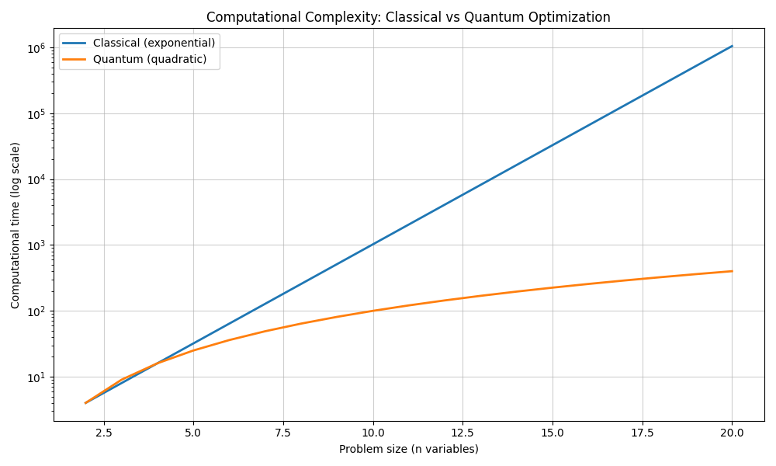
Cette dissymétrie n’est pas qu’un jeu de courbes. Elle reflète une asymétrie structurelle : alors que le calcul classique manipule des bits isolés, chacun étant dans un état déterminé (0 ou 1), le calcul quantique repose sur des qubits en superposition, capables de représenter plusieurs états simultanément. Et surtout, grâce au phénomène d’intrication, les qubits peuvent encoder collectivement des corrélations qu’aucun bit classique ne peut répliquer. C’est ce que nous allons explorer dans la seconde partie.
Le quantique, levier d’un nouvel espace computationnel
L’ordinateur quantique ne se contente pas d’accélérer les calculs : il transforme la manière même dont les solutions émergent. Contrairement aux approches classiques, qui explorent les possibilités les unes après les autres, les algorithmes quantiques exploitent la structure interne du problème en encodant simultanément un ensemble de réponses potentielles dans l’état du système. L’information n’est pas traitée de façon séquentielle, mais en parallèle, au sein d’un espace d’évolution fondamentalement différent. Cette dynamique repose sur un principe central : la manipulation des interférences. Bien orientées, celles-ci renforcent les trajectoires menant aux solutions pertinentes, tout en atténuant les autres.
Dans le domaine de l’optimisation globale, cette approche produit un avantage concret. Certains algorithmes quantiques, comme celui conçu par Grover, ont démontré qu’il est possible d’identifier une solution cible au sein d’un ensemble non structuré en mobilisant bien moins d’étapes que ne le permettrait une recherche classique. Même si ces gains sont aujourd’hui validés sur des systèmes de petite taille, ils témoignent d’un renversement du cadre de pensée : il ne s’agit plus d’ajouter de la puissance brute, mais de redéfinir l’architecture même de la recherche.
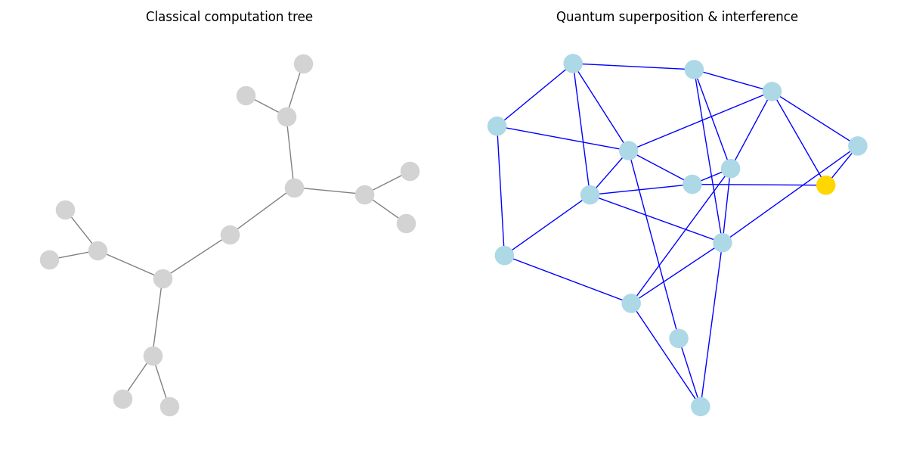
Ce paradigme devient particulièrement précieux lorsqu’il s’agit de résoudre des problèmes où les interdépendances entre variables rendent toute approche locale inefficace. Lorsque la solution globale ne peut être anticipée à partir des sous-parties, ou que la topologie du problème rend toute simplification hasardeuse, les circuits quantiques permettent d’intégrer l’ensemble du paysage de possibles au sein d’un processus cohérent. La capacité à faire émerger une solution sans devoir en parcourir chaque branche individuellement constitue l’un des apports majeurs du calcul quantique.
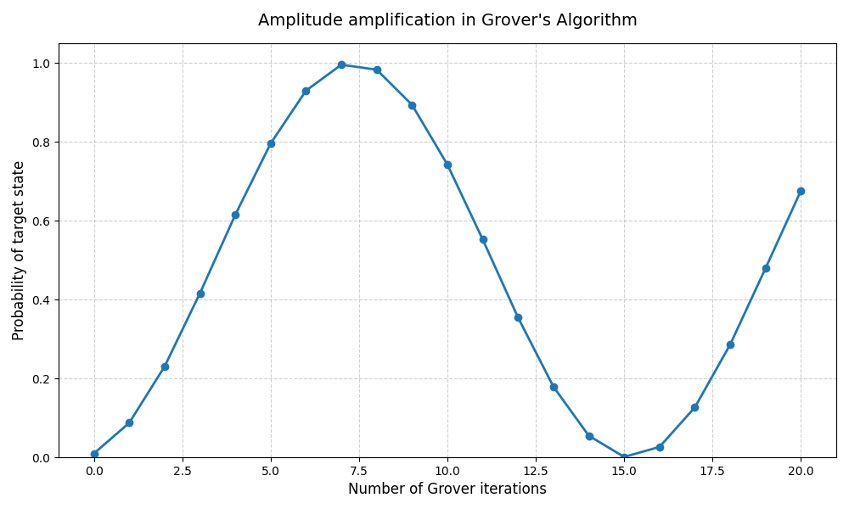
Les promesses portées par cette technologie ne résident donc pas dans une accélération uniforme de tous les calculs, mais dans une réorganisation profonde des règles du jeu. Là où l’ordinateur classique avance dans une arborescence de choix successifs, l’ordinateur quantique manipule les configurations globales en les faisant interagir. C’est une logique d’orientation, plus que de force brute.
Ce changement de perspective, bien qu’encore en construction à l’heure actuelle, dessine déjà les contours d’un nouvel horizon scientifique. Le calcul quantique ne remplace pas les approches existantes, il vient les compléter là où elles s’essoufflent et ne permettent pas d’obtenir des réponses. Dans les champs de la cryptographie, de la simulation moléculaire ou de l’optimisation combinatoire, il introduit des outils qui n’existaient pas et à mesure que les capacités technologiques progressent, ce ne sont pas uniquement les performances qui se redessinent, mais les types de questions que nous pouvons désormais poser.
Dans cette nouvelle géographie computationnelle, le défi n’est plus tant de franchir les limites actuelles que de repenser les chemins possibles. L’exploration du complexe ne passe plus par l’élimination du détail, mais par l’intégration active de l’ensemble des configurations.









